Un cilindro circular recto de radio r está inscrito en una esfera de radio 2r. Determine una

VIDEO ANSWER: Un cilindro circular recto está inscrito en una esfera de radio r. Encuentre el volumen más grande posible de este cilindro.
Área de una esfera vs Área lateral de un cilindro (sorprendente) YouTube

PROBLEMA RESUELTO 4. Se inscribe un cilindro circular recto dentro de una esfera de radio 8 cm, como se muestra en la figura. Si la altura del cilindro es el doble de su diámetro, calcule el volumen del cilindro.
Volúmen del Cono, Cilindro y Esfera YouTube

4. Encuentra el radio a partir del área superficial. Usa la fórmula r = √ (A/ (4π)). El área superficial de una esfera se deriva de la ecuación A = 4πr2. Encontrar la variable r te da √ (A/ (4π)) = r, lo que significa que el radio de una esfera es igual a la raíz cuadrada del área superficial dividida entre 4π.
Un cilindro circular recto de radio r está inscrito en una esfera de radio 2r. Determine una

Se tiene un cilindro inscrito en una esfera. Si la altura del cilindro es igual al radio de la esfera, y el volumen de la esfera es 288π cm3, calcular el vol.
DIBUJO TÉCNICO IES SAN ISIDORO Secciones planas de cono, cilindro y esfera.

Calcular el área y el volumen de cilindros, conos, esferas y pirámides regulares. Resolver problemas de solidos inscritos y circunscritos. Resolver problemas en los cuales los modelos se construyen utilizando las fórmulas de áreas y volúmenes de sólidos. En ésta sección se estudiará como calcular el volumen y el área del cilindro, el.
Calcule el Volumen de un cilindro inscrito en una esfera de radio 2R, si el radio del cilindro

Mas ejemplos: https://www.youtube.com/playlist?list=PL9SnRnlzoyX1Iczh6ssp4N36eDPlhwpoICurso de derivadas: https://www.youtube.com/playlist?list=PL9SnRnlzoyX1.
9 (a) Esfera de radio R. (b) Hemisferio de radio R. Download Scientific Diagram

A continuación, se presenta un método paso a paso para calcular el radio de un cilindro. Contenidos ocultar. 1 Paso 1: Entender la fórmula del volumen del cilindro. 1.1 Paso 2: Despejar r en la fórmula del volumen. 2 Paso 3: Identificar el volumen y la altura del cilindro. 2.1 Paso 4: Medir la altura del cilindro.
Cilindros conos y esferas YouTube

El video explica cómo determinar el volumen de un cilindro que se encuentra dentro de una esfera con las siguientes condiciones:Se inscribe un cilindro circu.
2.5 Volumen de la esfera (Cuaderno de ejercicio Resuelve) YouTube

4. Un cilindro circular recto está inscrito en una esfera de radio R. Determine el área superficial más grande… Recibe ahora mismo las respuestas que necesitas!
3 formas de encontrar el radio de una esfera wikiHow

VIDEO ANSWER: Se inscribe un cilindro circular recto en una esfera de radio r. Encuentre el volumen más grande posible de ese cilindro.
RADIO DE UN CILINDRO YouTube

#profenini te explica paso a paso como encontrar el volumen de la esfera circunscrita en un cilindro circular conociendo la altura y el diámetro de dicho cil.
COMO CALCULAR EL RADIO DE UNA ESFERA CON EL AREA O SUPERFICIE YouTube

El ing Luis Torres explica acerca de cilindros inscritos en una esfera
Volumen de una esfera conociendo radio o diámetro YouTube

Grafica una esfera de radio "r" y señala sus elementos en cada caso: r = 3 cm. r = 3,5 cm. r = 4 cm. r = 2 cm. Grafica. cilindro cuyo radio es "r" y altura "h". Además, señala sus elementos para el primer cilindro: r = 2 cm.
Optimizacion Volumen maximo de cilindro inscrito en una esfera YouTube

Math. Calculus. Question. Un cilindro circular recto está inscrito en una esfera de radio r r. Encuentre el mayor volumen posible de dicho cilindro. Solution.
3 formas de encontrar el radio de una esfera wikiHow

Encuentre el cilindro circular recto de mayor superficie que puede inscribirse en una esfera de radio r.Explico el ejercicio paso a paso mediante el cálculo.
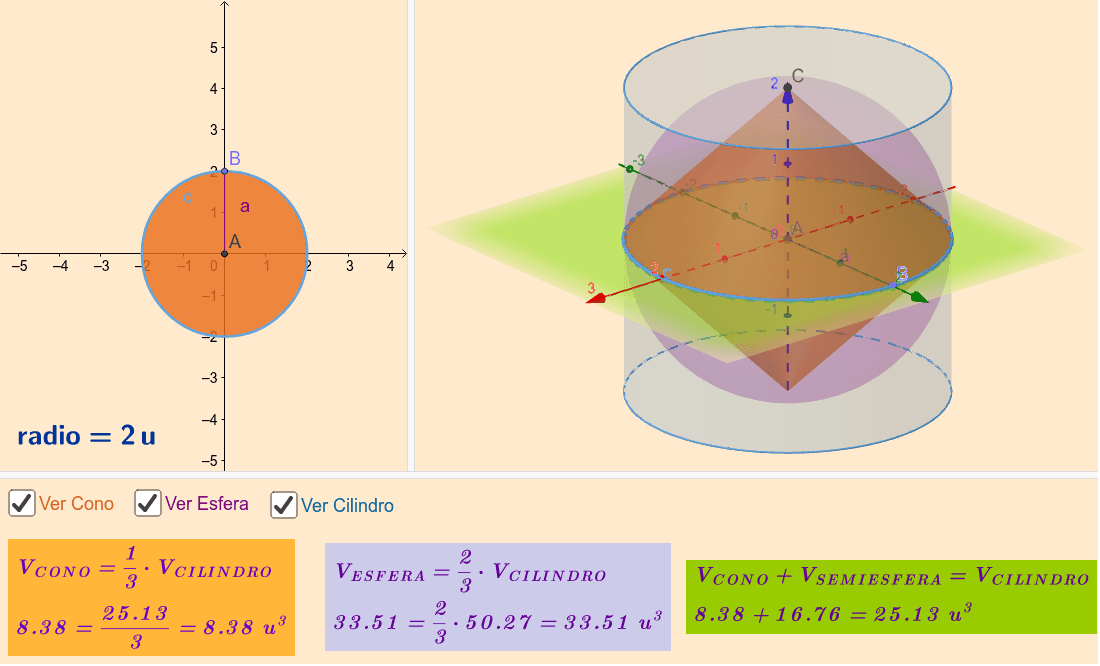
Relación entre los volumenes del cono, la esfera y el cilindrol cilindro GeoGebra
Hola , en este video estaremos resolviendo un problema el cual nos dice "SE CIRCUNSCRIBE UN CILINDRO CIRCULAR RECTO A UNA ESFERA DE RADIO R. ENCUENTRE EL ÁRE.
.
